Những thuật toán sắp xếp mảng trong lập trình

Xin chào mừng bạn đến với blog thủ thuật lập trình, hôm nay mình sẽ giới thiệu cho các bạn một trong những thuật toán lập trình thường hay áp dụng nhiều nhất trong thực tiễn cũng như trong học tập.

Thuật toán sắp xếp là gì?

Sắp xếp là quá trình bố trí lại các phần tử trong một tập hợp theo một trình tự nào đó nhằm mục đích giúp quản lý và tìm kiếm các phần tử dễ dàng và nhanh chóng hơn.

Tại sao phải sử dụng thuật toán sắp xếp

• Để có thể sử dụng thuật toán tìm nhị phân
• Để thực hiện thao tác nào đó được nhanh hơn

Những phương pháp sắp xếp bằng thuật toán.

• Phương pháp Đổi chỗ trực tiếp (Interchange sort)
• Phương pháp Nổi bọt (Bubble sort)
• Phương pháp Chèn trực tiếp (Insertion sort)
• Phương pháp Chọn trực tiếp (Selection sort)

I. Phương pháp Đổi chỗ trực tiếp (Interchange sort)

Sử dụng

Xét một mảng các số a[0], a[1], … a[n-1]

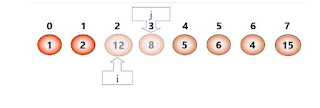
Nếu có i<j và a[i] > a[j], thì ta gọi đó là một nghịch thế

Mảng chưa sắp xếp sẽ có nghịch thế

Mảng đã có thứ tự sẽ không chứa nghịch thế

a[0] <= a[1] <=… <=[n -1]

Ý tưởng

Xuất phát từ đầu dãy, tìm tất cả nghịch thế chứa phần tử này, triệt tiêu chúng bằng cách đổi chỗ phần tử này với phần tử tương ứng trong cặp nghịch thế

Lặp lại xử lý trên với các phần tử tiếp theo trong dãy

Nhận xét.

Để sắp xếp một dãy số, ta có thể xét các nghịch thế có trong dãy và làm triệt tiêu dần chúng đi

Phương thức sử dụng.

void Swap(int &a, int &b){

    int temp = a;

    a = b;

    b = temp;

}

void InterchangeSort(int a[], int n){

    for (int i = 0; i < n - 1; i++)

        for (int j = i + 1; j < n; j++)

        if(a[i] > a[j])  //nếu có nghịch thế thì đổi chỗ

        Swap(a[i], a[j]);

}

II. Phương pháp Nổi bọt (Bubble sort)

Ý tưởng:

Xuất phát từ cuối dãy, đổi chỗ các cặp phần tử kế cận để đưa phần tử nhỏ hơn trong cặp phần tử đó về vị trí đầu dãy hiện hành, sau đó sẽ không xét đến nó ở bước tiếp theo

Ở lần xử lý thứ i có vị trí đầu dãy là i

Lặp lại xử lý trên cho đến khi không còn cặp phần tử nào để xét

Hàm BubbleSort

void BubbleSort(int a[], int n){

for (int i = 0; i < n - 1; i++)

for (int j = n - 1; j > i; j--)

   if(a[j] < a[j-1])

       Swap(a[j], a[j-1]);

}

III. Phương pháp Chèn trực tiếp (Insertion sort)

Nhận xét:

Mọi dãy a[0] , a[1] ,..., a[n-1] luôn có i-1 phần tử đầu tiên a[0] , a[1] ,... , a[i-2] đã có thứ tự (i ≥ 2)

Ý tưởng chính:

Tìm cách chèn phần tử a[i] vào vị trí thích hợp của đoạn đã được sắp để có dãy mới a[0] , a[1] ,... , a[i-1] trở nên có thứ tự

Vị trí này chính là pos thỏa : a[pos-1] <= a[i ]< a[pos] (1 <= pos <= i)

void InsertionSort(int a[], int n){

int pos, x;

for(int i = 1; i < n; i++){ //đoạn a[0] đã sắp

x = a[i]; 

pos = i;

while(pos > 0 && x < a[pos-1]){

a[pos] = a[pos-1]; // dời chỗ

pos--;

}

a[pos] = x;

}

}

IV. Phương pháp Chọn trực tiếp (Selection sort)

Nhận xét:

Mảng có thứ tự thì a[i] = min(a[i], a[i+1], …, a[n-1])

Ý tưởng: mô phỏng một trong những cách sắp xếp tự nhiên nhất trong thực tế:

Chọn phần tử nhỏ nhất trong n phần tử ban đầu, đưa phần tử này về vị trí đúng là đầu dãy hiện hành

Xem dãy hiện hành chỉ còn n-1 phần tử của dãy ban đầu, bắt đầu từ vị trí thứ 2; lặp lại quá trình trên cho dãy hiện hành... đến khi dãy hiện hành chỉ còn 1 phần tử

void SelectionSort(int a[], int n)

{

int min; // chỉ số phần tử nhỏ nhất trong dãy hiện hành

for (int  i = 0; i < n - 1; i++){

min = i; 

for(int j = i + 1; j < n; j++)

       if (a[j] < a[min])

       min = j; // ghi nhận vị trí phần tử nhỏ nhất

if (min != i)

       Swap(a[min], a[i]);

}

}